Daily 6 - Feb 4
Class Performance
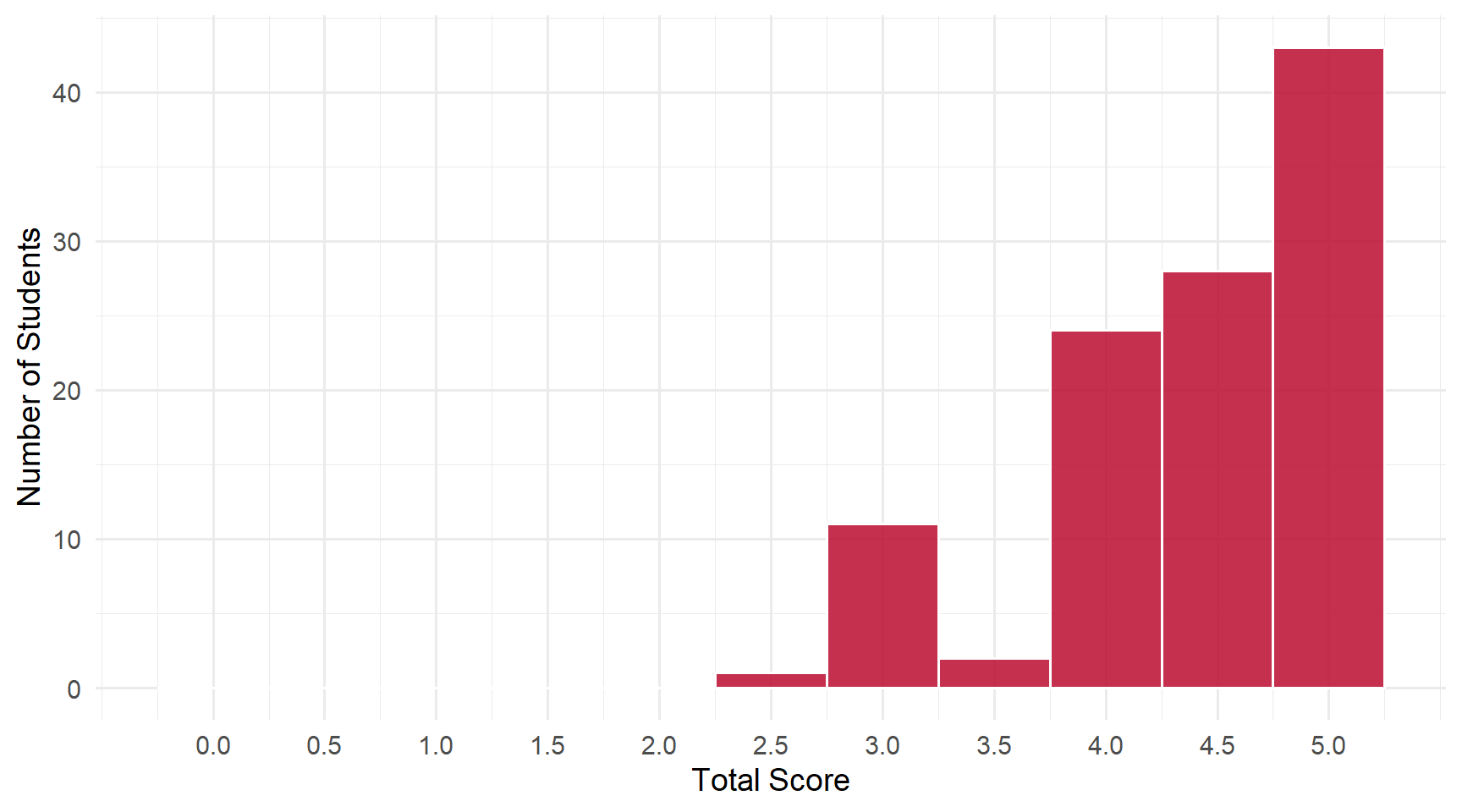
Students: 109 | Mean: 4.40 | Median: 4.5 | SD: 0.66
Scores ranged from 2.5 to 5 out of 5 points.
Score Distribution
Performance by Question
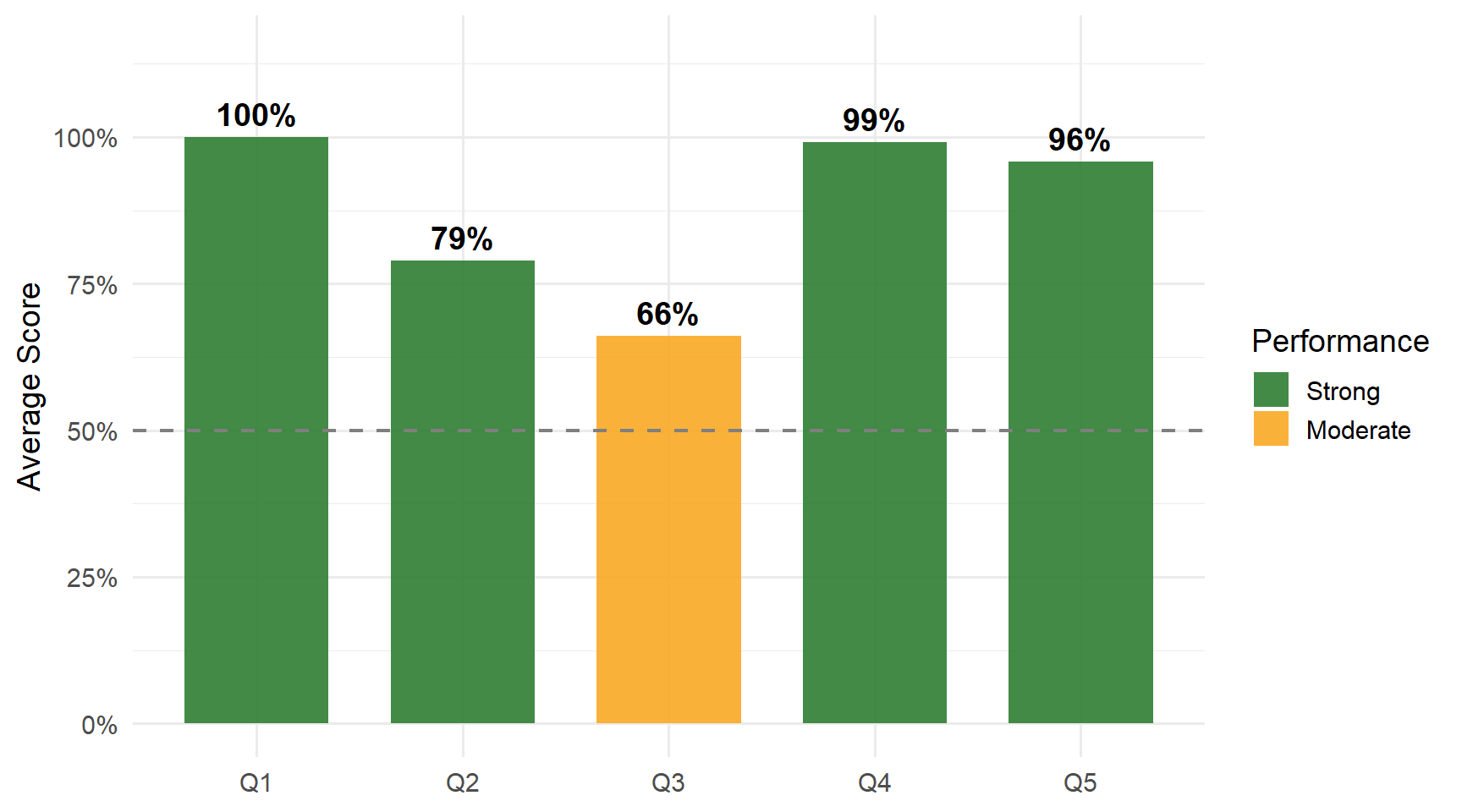
Questions
Q1: Estimating variance — plug in _____ for E(X) and replace outer expectation with sample _____
\(\overline{X}\) (sample average); average — Plug in the sample mean for \(E(X)\) and replace the outer expectation with another sample average.
- Near-universal success — Almost every student correctly identified \(\overline{X}\) and “average.”
- Minor notation variants — Some wrote “x-bar” or “mean(x)” instead of \(\overline{X}\); all accepted as equivalent.
- No significant errors observed — This was the strongest question across the class.
Q2: True or false — if an estimator is unbiased, then it will equal the estimand
False. An unbiased estimator equals the estimand on average across repeated samples, not necessarily for any single estimate.
- Answering “True” — The most common error. Students confused “unbiased on average” with “always equals the true value.”
- Crossed-out corrections — Several students initially wrote one answer then changed, suggesting uncertainty about this concept.
- Key distinction — Any single estimate can differ from the estimand due to sampling variability; unbiasedness is a property of the sampling distribution.
Q3: Explain what summarise does in the “Estimating the CEF” code chunk
It computes the sample average of earnings for each age group — estimating the conditional expectation function (CEF).
- Missing “by age” — Many mentioned “mean earnings” or “average” but omitted that it groups by age. The grouping is central to estimating the CEF.
- Too vague — Answers like “simplifies the data,” “creates a table,” “displays data better,” or “compiles data” don’t capture the computational step.
- Describing the concept, not the computation — Some wrote about “conditional expectations” abstractly without stating the specific operation: computing mean earnings grouped by age.
Q4: The estimated CEF in Figure 6 has a _____ shape
Concave — The estimated CEF shows a concave (inverted U) relationship between age and earnings.
- Near-universal success — Almost every student correctly identified the concave shape.
- Rare error: “variance” — One student wrote “variance” instead of describing the shape.
- No other significant errors — This was one of the strongest questions alongside Q1.
Q5: That shape is well-fit by a _____ in age
Quadratic — The concave shape is well-fit by a quadratic (second-degree polynomial) in age.
- Answering “polynomial” — While quadratic is a polynomial, the specific answer is quadratic. “Polynomial” is too broad.
- Answering “increase” or “condition” — These don’t describe a functional form.
- Overall strong performance — The vast majority correctly identified “quadratic.”
Key Takeaways
Strengths: Variance estimation plug-ins (Q1), concave CEF shape (Q4), quadratic fit (Q5).
Review:
- Unbiased ≠ always correct — unbiased means correct on average across samples, not for every single estimate
summarisecomputes average earnings by age — not just “displays” or “organizes” data; it calculates the mean within each group- Be specific about functional forms — “quadratic” is more precise than “polynomial”