Daily 8 - Feb 11
Class Performance
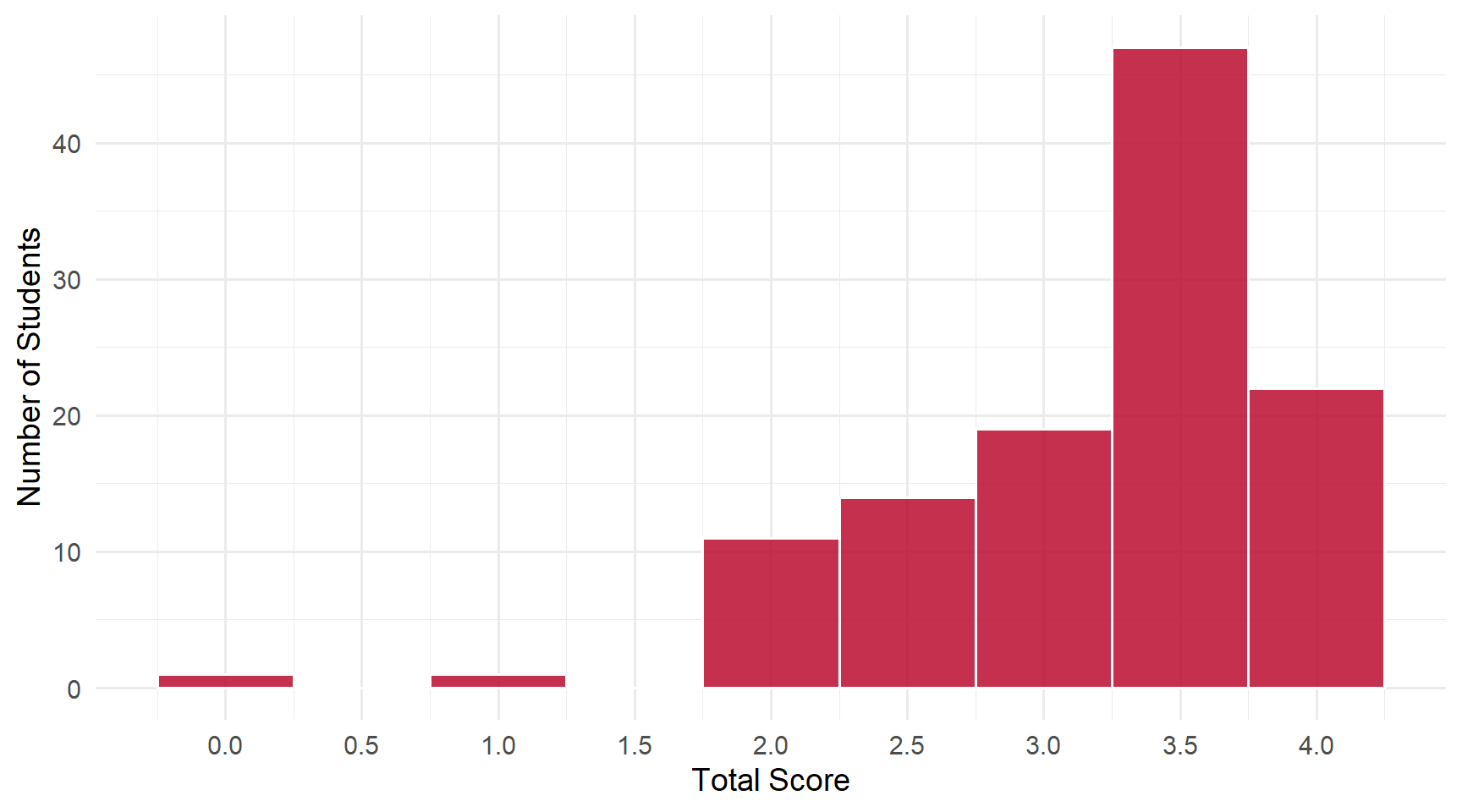
Students: 115 | Mean: 3.20 | Median: 3.5 | SD: 0.71
Scores ranged from 0 to 4 out of 4 points.
Score Distribution
Performance by Question
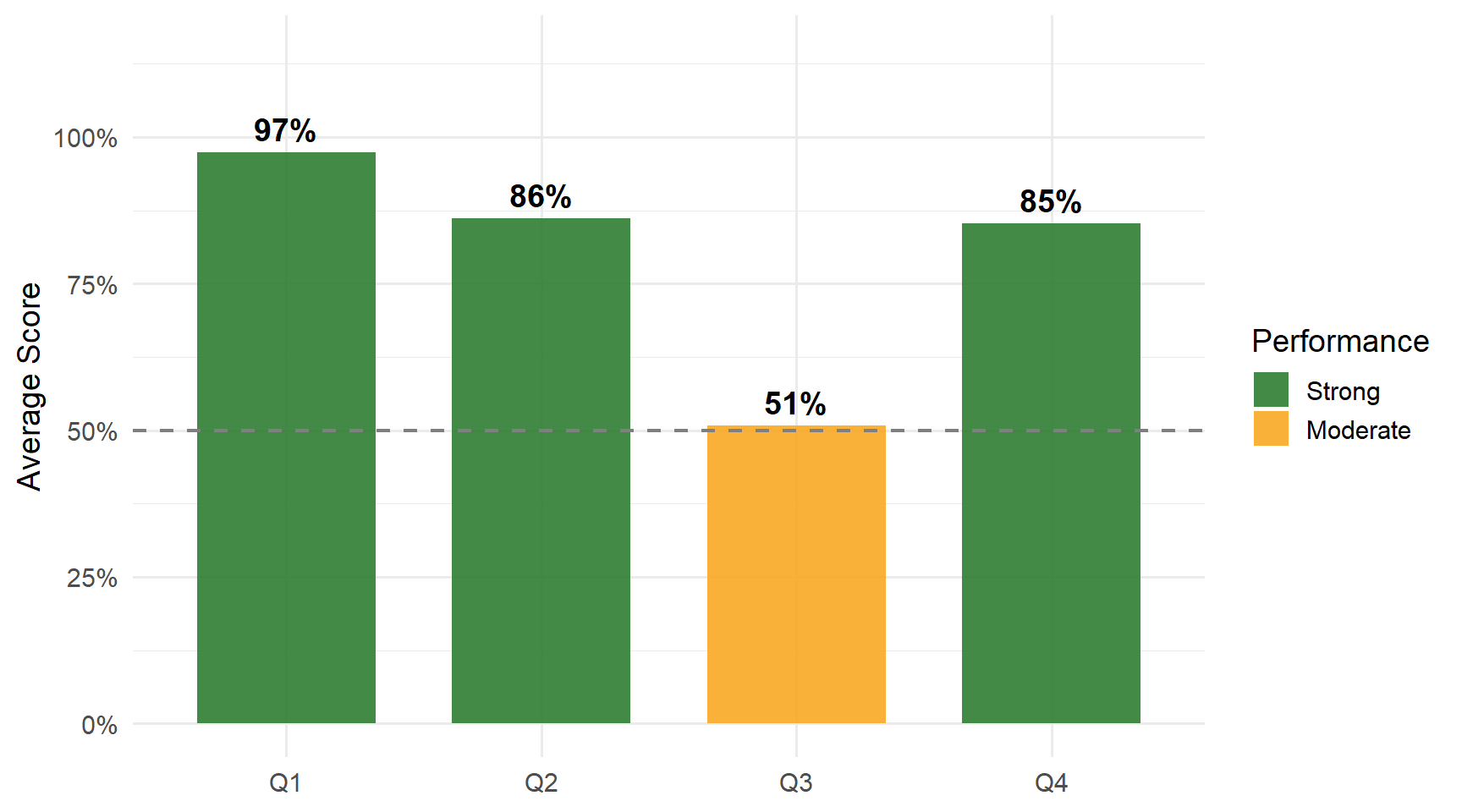
Questions
Q1: Good estimators approach the _____ as sample size increases
Estimand — good estimators approach the estimand (the target quantity being estimated) as sample size increases.
- Wrote “estimate” — An estimate is the value computed from a particular sample; the estimand is the target quantity. Close but distinct concepts.
- Wrote “parameter” or “the parameter” — Related concept, but the precise term is “estimand.” Not all estimands are traditional parameters.
- Wrote “mean” or “population mean” — The mean is one specific estimand, but the general answer is “estimand” — the target quantity for any estimator.
Q2: Good estimators have sampling distributions that approach the _____ distribution
Normal — good estimators have sampling distributions that approach the normal distribution as sample size increases (Central Limit Theorem).
- Wrote “sampling” — The sampling distribution is the distribution itself, not what it approaches. It approaches the normal distribution.
- Wrote “population” — The sampling distribution does not approach the population distribution. By the CLT, it approaches the normal distribution regardless of the population shape.
- Wrote “standard” or “approx normal” — The precise answer is simply “normal.” The CLT guarantees convergence to the normal distribution.
Q3: The standard error is the square root of the estimated variance of its _____ distribution
Sampling — the standard error is the square root of the estimated variance of the estimator’s sampling distribution.
- Wrote “sample” instead of “sampling” — The most common error. “Sample distribution” describes one dataset; “sampling distribution” describes the distribution of the estimator across all possible samples.
- Wrote “normal” or “standard” — While the sampling distribution may approach normal, the question asks which distribution’s variance defines the SE — that’s the sampling distribution.
- Wrote the SE formula instead of the word — The question asks for the type of distribution (one word: “sampling”), not the formula itself.
Q4: Formula for the standard error of the sample average
se(\(\overline{Y}\)) = \(\sqrt{s^2/N}\) — the square root of the sample variance divided by the sample size. Equivalently, \(\sqrt{\widehat{\text{var}}(\overline{Y})}\).
- Wrote the sample variance formula instead of SE — s\(^2\) = 1/(N-1)\(\sum\)(Y\(_i\)-\(\overline{Y}\))\(^2\) is the variance, not the standard error. The SE is \(\sqrt{s^2/N}\).
- Wrote the sample mean formula — \(\overline{Y}\) = 1/N \(\sum\) Y\(_i\) is the sample average, not the standard error formula.
- Missing the square root — Writing var\((\overline{Y})\) = s\(^2\)/N gives the variance, not the SE. The SE requires the square root: \(\sqrt{s^2/N}\).
Key Takeaways
Strengths: Nearly all students correctly identified “estimand” for Q1 | Strong performance on Q2 (normal distribution) | Most students wrote the SE formula correctly.
Review:
- “Sampling” vs. “sample” distribution — the most common error; these are distinct concepts
- SE formula = \(\sqrt{s^2/N}\) — equivalently \(\sqrt{\widehat{\text{var}}(\overline{Y})}\); don’t confuse with the variance formula itself
- Normal vs. sampling — the sampling distribution approaches the normal distribution (don’t swap these answers)